Can you embroider the Night Watch in 10 years?
— last updated
My wife is working on an embroidery project to recreate The Night Watch by Rembrandt. She wants to finish within 10 years. Because I like this type of thing I offered to help calculate if she was still on track.

The instruction divides the image into 96 pieces.
import os
import matplotlib.pyplot as plt
import matplotlib.dates as mdates
from nachtwacht import date_from_filename, get_finished_parts, TOTAL_PARTS
from sklearn import linear_model
import numpy as np
from datetime import datetime
get the files from the existing blogposts.
image_folder = "../content/nachtwacht/"
files = [os.path.abspath(os.path.join(image_folder, f)) for f in os.listdir(image_folder) if f.startswith("nachtwacht")]
posts = [(f, date_from_filename(f), get_finished_parts(f)) for f in sorted(files)]
dates = [d for (_,d,_) in posts]
def to_timestamp(date):
return datetime.combine(date, datetime.min.time()).timestamp()
def dates_to_timestamps(dates):
timestamps = [to_timestamp(d) for d in dates]
timestamps = np.array(timestamps).reshape(-1, 1)
return timestamps
timestamps = dates_to_timestamps(dates)
finished_parts = [fp for (_,_,fp) in posts]
Use a standard linear model
lm = linear_model.LinearRegression()
model = lm.fit(timestamps,finished_parts)
def plot_graph(model, dates, finished_parts):
timestamps = dates_to_timestamps(dates)
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(dates, finished_parts)
ax.plot(dates, model.predict(timestamps), color='red')
ax.xaxis.set_major_formatter(mdates.DateFormatter('%Y-%m'))
plt.xticks(rotation=45)
Fit the linear model on all dates / finished parts
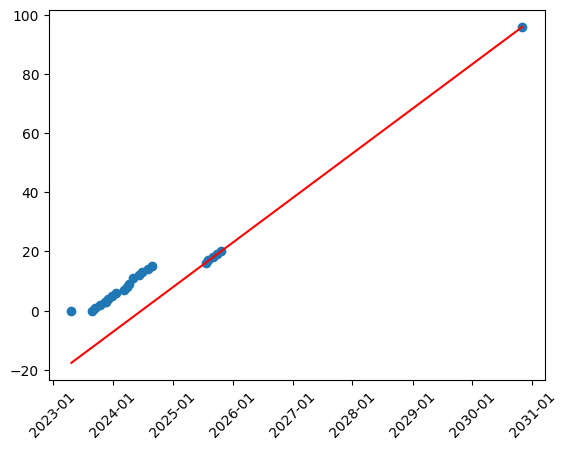
plot_graph(model, dates, finished_parts)
Notice the gap between the summer of 2024 and 2025? You can read on her blog what happened that caused the lack of progress.
def calculate_end_date(model):
m = model.coef_[0] # The coefficient (slope)
b = model.intercept_ # The intercept
required_x = (TOTAL_PARTS - b) / m
required_x
end_date = datetime.fromtimestamp(required_x)
print("Predicted end date:", end_date.date())
return end_date
end_date = calculate_end_date(model)
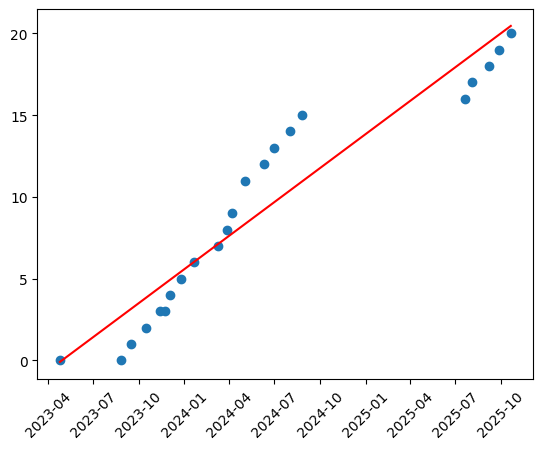
Predicted end date: 2034-12-16
plot_graph(dates + [end_date], finished_parts + [TOTAL_PARTS])
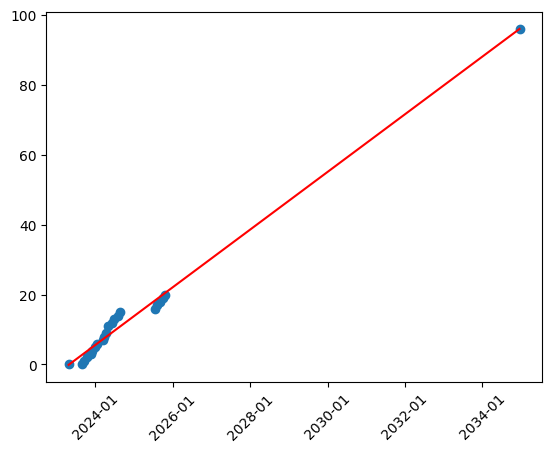
consider only the most recent 5 posts
model = lm.fit(dates_to_timestamps(dates[-5:]),finished_parts[-5:])
end_date = calculate_end_date(model)
plot_graph(dates + [end_date], finished_parts + [TOTAL_PARTS])
Predicted end date: 2030-10-31
Let’s hope it will be finished in 2030!